Qin, Yang, Zhuang, Long, Yang, and Zhang: Morphological and Hemodynamic Parameters for Middle Cerebral Artery Bifurcation Aneurysm Rupture Risk Assessment
Abstract
Objective
To investigate the morphological and hemodynamic parameters associated with middle cerebral artery (MCA)bifurcation aneurysm rupture.
Methods
A retrospective study of 67 consecutive patients was carried out based on 3D digital subtraction angiography data. Morphological and hemodynamic parameters including aneurysm size parameters (dome width, height, and perpendicular height), longest dimension from the aneurysm neck to the dome tip, neck width, aneurysm area, aspect ratio, Longest dimension from the aneurysm neck to the dome tip (Dmax) to dome width, and height-width, Bottleneck factor, as well as wall shear stress (WSS), low WSS area (LSA), percentage of LSA (LSA%) and energy loss (EL) were estimated. Parameters between ruptured and un-ruptured groups were analyzed. Receiver operating characteristics were generated to check prediction performance of all significant variables.
Results
Sixty-seven patients with MCA bifurcation aneurysm were included (31 unruptured, 36 ruptured). Dmax (p=0.008) was greater in ruptured group than that in un-ruptured group. D/W (p<0.001) and the percentage of the low WSS area (0.09±0.13 vs. 0.01±0.03, p<0.001) were also greater in the ruptured group. Moreover, the EL in ruptured group was higher than that in un-ruptured group (6.39±5.04 vs. 1.53±0.86, p<0.001). Multivariate regression analysis suggested D/W and EL were significant predictors of rupture of MCA bifurcation aneurysms. Correlation analyses revealed the D/W value was positively associated with the EL (R=0.442, p<0.01).
Conclusion
D/W and EL might be the most two favorable factors to predict rupture risk of MCA bifurcation aneurysms.
Key Words: Biomarkers · Middle cerebral artery aneurysm · Risk assessment · Receiver operating characteristics curve · Angiography · Digital subtraction.
INTRODUCTION
The incidence of cerebral aneurysms is difficult to estimate 1). Un-ruptured intracranial aneurysms are mostly located in the middle cerebral artery (MCA), with 80-83% occupying at the bifurcation. According to the database by Dashti et al. 4), the bifurcation aneurysms of MCA consists of the most ruptured aneurysms. Major rupture is the most frequent presentation of cerebral aneurysms, most commonly produces subarachnoid hemorrhage, a catastrophic event with high morbidity and mortality 2). Unlike ruptured aneurysms, there is controversy and uncertainty around the treatment of asymptomatic un-ruptured aneurysms among practitioners with similar specialized practice 3). For this reason, the evaluation of rupture risks is crucial for the management once a un-aneurysm is diagnosed. Except the anatomical factors, morphological parameters were discussed based on digital subtraction angiography (DSA) as predictors of aneurysm rupture recently. Literatures studied mainly on variable such as size, neck width, aspect ratio (AR), height-width (H/W) ratio, bottleneck factor etc. 1,6,7,9,12,15,16,19,32,33). Moreover, hemodynamics, such as wall shear stress (WSS), low WSS area (LSA), were also considered might contribute to aneurysm rupture 1,11,17,20-22,31,32). However, few studies had focused MCA bifurcation aneurysms in combining morphological and hemodynamic parameters. This study analyzed the differences of morphological and hemodynamic parameters between ruptured and un-ruptured aneurysms located on MCA bifurcation. Our aim was to identify the characteristics that might predict rupture tendency of these aneurysms.
MATERIALS AND METHODS
A total of 67 patients with MCA bifurcation aneurysm were included (31 un-ruptured, 36 ruptured) from multiple hospitals in Beijing during 2012 and 2015. Local ethical committee approved the study and consents from Patients were acquired. All patients accepted cerebral digital subtraction angiography (cDSA, Innova4100; GE Medical Systems SCS, Buc, France) after admitted to the hospital, and raw data were processed in GE Work Station AW 4.5/4.6 (GE Medical Systems, Chicago, IL, USA).
Morphological parameters were measured from 3D-DSA, including aneurysm size parameter, such as Dmax (longest dimension from the aneurysm neck to the dome tip), neck width (average diameter of the aneurysm neck, N), height (maximal height from dome tip perpendicular to aneurysm neck, H), dome width (maximal diameter perpendicular to Dmax, W), and aneurysm (AN) area. AR was calculated by dividing dome height (ARh) or Dmax (ARd) by neck width. D/W was defined as Dmax to dome width. And H/W ratio was also calculated by dividing height by dome width. Bottleneck factor was defined as the ratio of dome width to neck width.
For hemodynamic analysis, 3D models were generated with raw DICOM data and processed using MIMICS 14.11 (Materialise Group, Leuven, Belgium) and Geomagic studio 12.0 (Raindrop Geomagic Corporation, Rock Hill, SC, USA), remaining AN and parent artery, saved as standard tessellation language format for further processing. The workstation of Workbench software was run with two Intel® Xeon® processors of 3.1 GHz, a Windows operating system (version 7; JFC Group, Auckland, Australia) and a DR3 of 8 GB. The modified models were imported into ICEM CFD 14.5 (ANSYS, Canonsburg, PA, USA) and transformed into finite volume meshes of 1 million elements for computational fluid dynamics (CFD) simulations to calculate time-resolved 3D velocity and pressure fields 23,34). In order to simulate realistic condition of blood flow, 3 prism layers quadrilateral meshes with equal sides were installed next to the wall of vessels and aneurysms. Two pulsatile cycles were simulated with the mesh models using ANSYS CFX 5 (ANSYS), and the maximum stenosis time of the second cycle was documented. From the flow solutions, WSSs, LSA, percentage of LSA (LSA%) and energy loss (EL) were calculated. WSS is tangential frictional stress caused by blood flow on the vessel wall 27,28). WSSmax and WSSmin is the maximum and minimum time-averaged aneurysmal WSS magnitude, respectively. In the statistical analysis, we averaged WSS (WSSave) over the WSSmax and the WSSmin. LSA is defined as areas of the aneurysm wall exposed to WSS below 10% of the mean parent arterial WSS 30). Percentage of LSA is the ratio between LSA and AN area. The EL of aneurysms in the simulation was described as the difference between the “with-aneurysm” and “pre-aneurysm” conditions ( Formula 1). According to Bernoulli Equation, energy was calculated as formula 2. When there were multiple inlet and outlets, the EL was calculated by subtracting two outlet bifurcation arteries from the inlet M1 segment of MCA as formula 3. As a result, EL in this study was EL1 (EL from M1 segment of MCA) subtracting the sum of EL2 (EL from M2 segment of MCA) and EL3 (EL from M3 segment of MCA). V presents the blood velocity of the test plane, A is the area of the test plane, ρ is the blood density, P stands for the static blood pressure of the test plane.
Statistical analysis
All data were presented with mean and standard deviation, and used Kolmogorov-Smirnov test for distribution characteristic. Student t-test was employed for normal distribution variables for the differences between ruptured and un-ruptured groups, and Mann-Whitney U test for non-normal distribution variables. All significant morphological and hemodynamic variables were added to the multivariate logistic regression using stepwise addition mode. To identify optimal thresholds for IA rupture, receiver operating characteristics (ROC) analysis was applied to significant variables. Area under the ROC (AUC-ROC) was also calculated to check the performance of significant variables in prediction of aneurysm rupture. Pearson’s correlation was further analyzed within significant variables in the multivariate model. The level p<0.05 was considered statistically significant. All the data were analysis with SPSS ver. 22.0 (SPSS Inc., Chicago, IL, USA).
RESULTS
Analysis had run for all variables according to data distribution and results were submitted in Table 1 and Fig. 1. Across all the variables, Dmax ( p=0.008), Aspect ratio according to Dmax (ARd, p=0.012), H/W ( p<0.001), D/W ( p<0.001) were greater in ruptured group. However, ruptured group tended to have lower average wall shear stress (WSSave) than that in the un-ruptured (21.26±19.60 vs. 22.21±18.46, p=0.838), while definitely more LSA ([1.59±3.88]E-05 vs. [1.41±3.26]E-06, p=0.031) and LSA% (0.09±0.13 vs. 0.01±0.03, p<0.001). Un-ruptured group had less EL compared to ruptured group (1.53±0.86 vs. 6.39±5.04, p <0.001). Inlet energy from M1 segment of MCA (EL1) was also higher in ruptured group (22.96±16.13 vs. 15.35±9.58, p <0.025). In multivariate logistic regression, D/W was entered into the model on step 1 with p<0.001 and odd ratio of 8.525, which demonstrated a significant positive effect on aneurysm rupture. The overall prediction accuracy on the first step in this model was 85.1%. EL was entered to the model on step 2, which raised the overall prediction accuracy to 91.0%. The odd ratio for D/W (p=0.005) and EL (p=0.005) were 6.760 and 1.497 respectively, indicating D/W had a greater positive impact in this model than EL. The other variables were no statistically significant in the multivariate logistic regression.
ROC was generated and summarized in Figs. 2 and 3. The EL had the greatest AUC (0.931, p<0.001), followed by D/W (0.918, p<0.001) and LSA% (0.901, p<0.001), illustrating an excellent performance in predicting aneurysm rupture. H/W ( p<0.001) and LSA ( p<0.001) were also good in this model with AUC of 0.887 and 0.849, respectively. A possible optimal threshold for EL was 1.8450 in this analysis with a sensitivity of 0.917 and specificity of 0.774. The possible threshold for D/W was 1.015836 with a sensitivity of 0.889 and specificity of 0.774. As for LSA% was 0.0089250, with the sensitivity of 0.889 and specificity of 0.742. Further Spearman’s correlation analysis demonstrated D/W and EL showed had significant correlation for 0.442 (p<0.001).
DISCUSSION
Currently, aneurysm size was believed to associate with aneurysm rupture 7,33). A study of 1309 MCA aneurysms by Elsharkawy et al. 7) found most of the ruptured MCA aneurysms were 7 to 14 in size (55%) and located at the main bifurcation (77%). In this study, we use different parameters to consider aneurysm size. Data in this study showed the Dmax, not aneurysm height (H) tended to be associated with the rupture status. Alternative aneurysm size definitions have a significant impact on prediction performance and optimal threshold values. Adoption of standard methodology and sizing nomenclature appears critical to ensure rupture detection performance and reproducibility across studies 13). Moreover, most of the studies were focusing on aneurysm height and neck width, or morphological variable in relation with height such as AR. The AR was believed as a reliable predictor in aneurysm rupture. 7) And aneurysm size was not significant while AR was significant, which is consistent with other studies 5,29,32). Some study showed AR was higher in rupture groups, suggesting a threshold value of 1.6 29), while our result showed ARh had the tendency to be higher, but without a statistic difference in the rupture group. Except the commonly discussed ARh, ARd was also calculated in this study, and was higher in the ruptured group. Moreover, the AUC-ROC and significant difference in the D/W made the D/W the strongest indicator among all the variables in this study, indicating Dmax or Dmax related parameter might be more appropriate in predicting aneurysm rupture. Low WSS was independently correlated with ruptured aneurysms, with the odds of rupture around 0.59 provided by logistic models by Xiang et al. 31,32) The maximum WSS tended to be near the neck of the aneurysm, while low WSSs located at the tip of ruptured aneurysms 24). Low WSS could promote atherogenesis and inflammatory cell infiltration 29), and cause degenerative changes and trigger the rupture of aneurysms 18). One study pointed that a low WSS may be associated with aneurysm ruptures, but without statistical significance in MCA groups 26). This correlate well with our results. Based on the data, there was no difference in WSS, but the percentage of low WSS area (LSA%) between un-ruptured and ruptured groups, indicating LSA% to be a better predictor in aneurysm rupture. These results supported previous studies in that low WSS and percentage of LSA might lead to aneurysm rupture 16,17,21,24,33). However, there is the controversy over low WSS or high WSS in predicting aneurysm rupture 25). In contrary to low WSS, high WSS might associate with the growth and rupture of small or secondary bleb aneurysm phenotypes in combination with a positive WSS gradient by triggering a mural-cell-mediated pathway 20). Although there is a potential mechanism of high WSS in aneurysm rupture, more reports suggested low WSS as a more significant predictor in aneurysm rupture. EL was recently introduced as a hemodynamic parameter to investigate the mechanism of aneurysm rupture. It had the ability to quantitatively calculate this energy loss due to blood flow passing through a given aneurysm and was shown to be one of the major factors involved in aneurysm initiation growth and rupture and be able to predict the rupture risk 23). Several studies have showed higher EL indicating high risk of aneurysm rupture 10,14). Aneurysms with increasing EL are more likely to rupture than those with decreasing EL 8). However, the published studies were either with small study samples, or based only on experimental models. This study provided clinical evidence with 67 aneurysms located at MCA bifurcation that more energy loss in the aneurysm area had significant correlation with higher risk of aneurysm rupture. The EL in un-ruptured aneurysm group and ruptured group had a statistic significant with a mean value of 6.39±5.04 and 1.53±0.86, respectively. Both in logistic regression model and ROC, EL played a major role in predicting aneurysm rupture. As the data showed, D/W was the most influential predictor, and also significant correlated with EL and LSA%. Moreover, it would be logical that the higher D/W presented in an aneurysm, the more energy will be consumed through the complicated unites. In return, the more energy had lost, it could be more likely to have a lower WSS, which might explain higher LSA and LSA% in ruptured group. On the other hand, the high LSA% could favorite the atherogenesis and inflammatory cell infiltration in the low WSS area as a pathological mechanism. As a result, the combination of morphological and hemodynamic parameters was appropriate in prediction of aneurysm rupture, especially with D/W, and EL.
There are some limitations in our study. Firstly, though it was a multi-center study for aneurysms located at MCA bifurcation, the number of samples was small. Secondly, we did not include demographic, genetic, pathologic, medial, shape changing factors in our study. We may extend the patient population and the parameters to validate our result in the future. Finally, our morphological and hemodynamic parameters were based on DSA in 3D region, which measurement bias could exist. Further automatic measurement should be employed to decrease this bias.
CONCLUSION
It was sensitive and optimal to use morphological and hemodynamic parameters in predicting the rupture of MCA bifurcation aneurysm. The D/W and EL might be considered to be the most two favorable factors in the prediction.
Acknowledgements
This work was supported by Capital Development Funds of Medical Science (20111001-01).
Fig. 1
Definition of morphological variables. 1: neck (N), the average diameter of the aneurysm neck, 3.65 mm; 2: Dmax, the longest dimension from the aneurysm neck to the dome tip, 5.14 mm; 3: height (H), maximal height from dome tip perpendicular to aneurysm neck, 1.67 mm; 4: dome width (W), the maximal diameter perpendicular to Dmax, 2.48 mm. Dmax: longest dimension from the aneurysm neck to the dome tip. 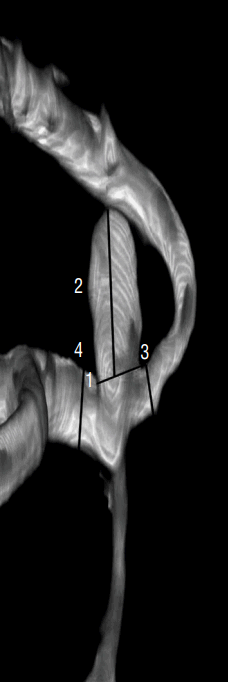
Fig. 2
Morphological and hemodynamic modelling of un-ruptured (A and B) and ruptured (C and D) MCA bifurcation aneurysms. A1 and B1, examples of refined morphological modelling in un-ruptured group; C1 and D1, examples of refined morphological modelling in ruptured group, which are larger in size than that in un-ruptured group; A2 and B2, hemodynamic simulations for un-ruptured aneurysms, presenting high velocity with red, which affect EL according to formula 2; C2 and D2, hemodynamic simulations for ruptured aneurysms, demonstrating more complex blood flow inside the aneurysms and more energy difference between in-let and out-let arteries; A3 and B3, the distribution of WSS in un-ruptured aneurysms; C3 and D3, the distribution of WSS in ruptured aneurysms with significant more low WSS area than that in un-ruptured group; A4 and B4, the percentage of LSA in un-ruptured aneurysm; C4 and D4, illustrate the LSA% are significantly higher in ruptured aneurysms. MCA: middle cerebral artery, EL: energy loss, WSS: wall shear stress, LSA: low WSS area. 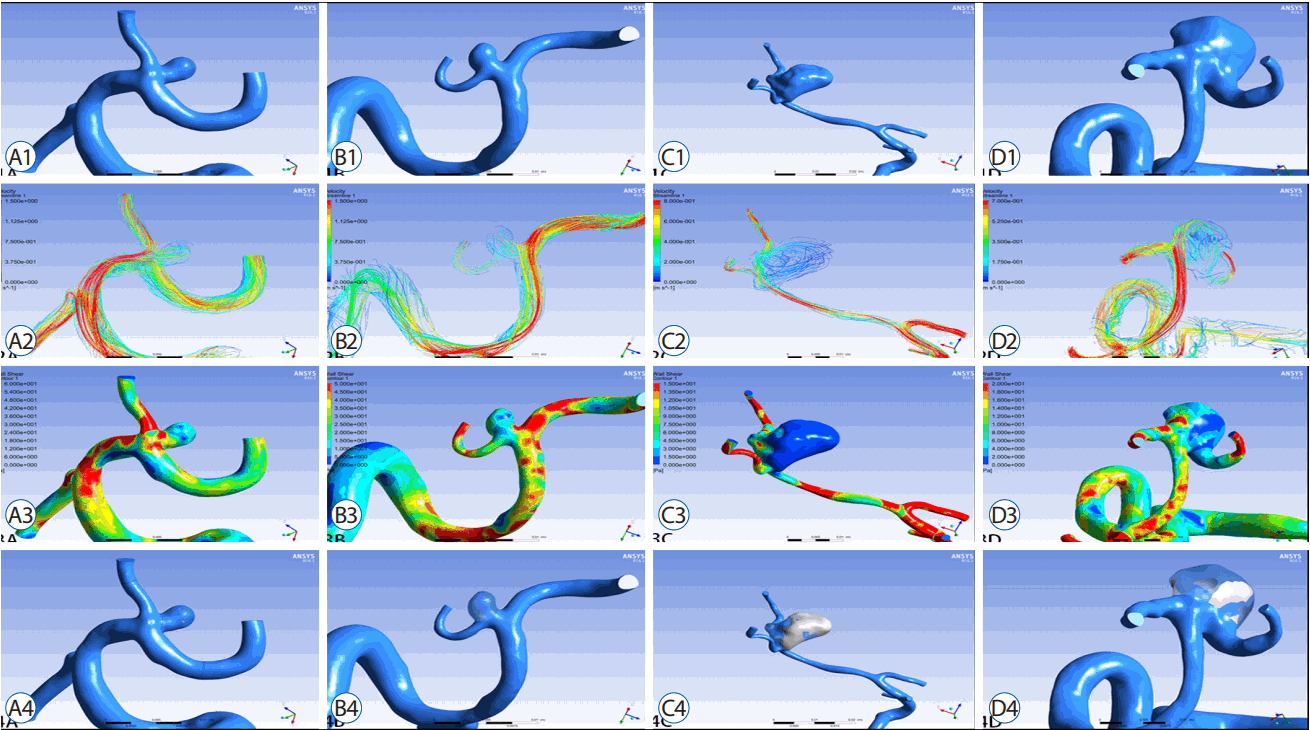
Fig. 3
The ROC curve for all significant variables predicting MCA bifurcation aneurysm rupture. ROC: receiver operating characteristics, MCA: middle cerebral artery, D/W: dome width, EL: energy loss, H/W: height-width, LSA: low wall shear stress area. 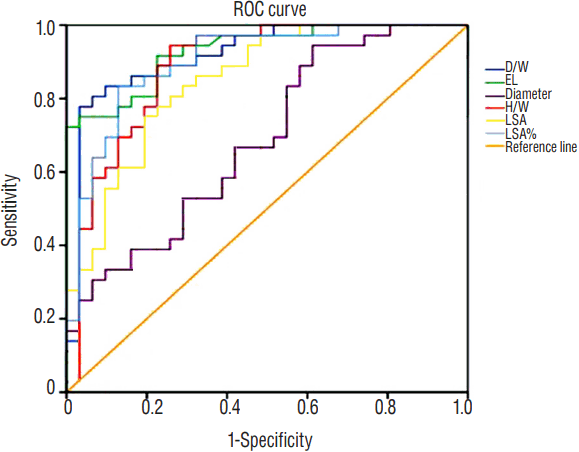
Table 1
Variables in ruptured and un-ruptured groups
|
Variable |
Mean±SD |
p-value |
|
Neck |
4.75±2.01 |
0.257 |
|
Height |
4.53±2.52 |
0.026*
|
|
Dmax |
5.33±2.98 |
0.008*
|
|
Width |
4.83±2.13 |
0.667 |
|
ARh=H/N |
0.98±0.49 |
0.072 |
|
ARd=D/N |
1.15±0.52 |
0.012*
|
|
H/W |
0.93±0.27 |
<0.001*
|
|
BNF=W/N |
1.05±0.31 |
0.048*
|
|
D/W |
1.11±0.36 |
<0.001*
|
|
WSSave |
21.69±18.95 |
0.838 |
|
WSSmax |
91.52±49.87 |
0.105 |
|
WSSmin |
0.86±2.22 |
0.382 |
|
LSA |
(9.22)E-06±2.92E-05 |
0.031*
|
|
AN area |
(9.97±9.28)E-05 |
0.145 |
|
LSA% |
0.056±0.104 |
0.001*
|
|
EL1 |
19.43±13.94 |
0.025*
|
|
EL2 |
9.00±7.33 |
0.289 |
|
EL3 |
6.30±7.42 |
0.651 |
|
EL |
4.14±4.44 |
<0.001*
|
References
1. Connolly ES Jr, Rabinstein AA, Carhuapoma JR, Derdeyn CP, Dion J, Higashida RT, et al : Guidelines for the management of aneurysmal subarachnoid hemorrhage: a guideline for healthcare professionals from the American Heart Association/American Stroke Association. Stroke 43 : 1711-1737, 2012   2. Cross DT 3rd, Tirschwell DL, Clark MA, Tuden D, Derdeyn CP, Moran CJ, et al : Mortality rates after subarachnoid hemorrhage: variations according to hospital case volume in 18 states. J Neurosurg 99 : 810-817, 2003   3. Darsaut TE, Estrade L, Jamali S, Bojanowski MW, Chagnon M, Raymond J : Uncertainty and agreement in the management of unruptured intracranial aneurysms. J Neurosurg 120 : 618-623, 2014   4. Dashti R, Hernesniemi J, Niemelä M, Rinne J, Porras M, Lehecka M, et al : Microneurosurgical management of middle cerebral artery bifurcation aneurysms. Surg Neurol 67 : 441-456, 2007   6. Duan G, Lv N, Yin J, Xu J, Hong B, Xu Y, et al : Morphological and hemodynamic analysis of posterior communicating artery aneurysms prone to rupture: a matched case-control study. J Neurointerv Surg 8 : 47-51, 2016   7. Elsharkawy A, Lehečka M, Niemelä M, Kivelev J, Billon-Grand R, Lehto H, et al : Anatomic risk factors for middle cerebral artery aneurysm rupture: computed tomography angiography study of 1009 consecutive patients. Neurosurgery 73 : 825-837; discussion 836-837, 2013    8. Farnoush A, Avolio A, Qian Y : A growth model of saccular aneurysms based on hemodynamic and morphologic discriminant parameters for risk of rupture. J Clin Neurosci 21 : 1514-1519, 2014   9. Fan J, Wang Y, Liu J, Jing L, Wang C, Li C, et al : Morphological-hemodynamic characteristics of intracranial bifurcation mirror aneurysms. World Neurosurg 84 : 114-120.e2, 2015   10. Hu P, Qian Y, Lee CJ, Zhang HQ, Ling F : The energy loss may predict rupture risks of anterior communicating aneurysms: a preliminary result. Int J Clin Exp Med 8 : 4128-4133, 2015   11. Jing L, Zhong J, Liu J, Yang X, Paliwal N, Meng H, et al : Hemodynamic effect of flow diverter and coils in treatment of large and giant intracranial aneurysms. World Neurosurg 89 : 199-207, 2016   12. Lall RR, Eddleman CS, Bendok BR, Batjer HH : Unruptured intracranial aneurysms and the assessment of rupture risk based on anatomical and morphological factors: sifting through the sands of data. Neurosurg Focus 26 : E2, 2009  13. Lauric A, Baharoglu MI, Malek AM : Ruptured status discrimination performance of aspect ratio, height/width, and bottleneck factor is highly dependent on aneurysm sizing methodology. Neurosurgery 71 : 38-45, 2012    14. Long Y, Zhong J, Yu H, Yan H, Zhuo Z, Meng Q, et al : A scaling aneurysm model-based approach to assessing the role of flow pattern and energy loss in aneurysm rupture prediction. J Transl Med 13 : 311, 2015    15. Lv N, Feng Z, Wang C, Cao W, Fang Y, Karmonik C, et al : Morphological risk factors for rupture of small (<7 mm) posterior communicating artery aneurysms. World Neurosurg 87 : 311-315, 2016   16. Lv N, Wang C, Karmonik C, Fang Y, Xu J, Yu Y, et al : Morphological and hemodynamic discriminators for rupture status in posterior communicating artery aneurysms. PLoS One 11 : e0149906, 2016    17. Lv N, Yu Y, Xu J, Karmonik C, Liu J, Huang Q : Hemodynamic and morphological characteristics of unruptured posterior communicating artery aneurysms with oculomotor nerve palsy. J Neurosurg 125 : 264-268, 2016   18. Malek AM, Alper SL, Izumo S : Hemodynamic shear stress and its role in atherosclerosis. JAMA 282 : 2035-2042, 1999   19. Maiti TK, Bir SC, Patra DP, Cuellar H, Nanda A : 158 morphological parameters for anterior communicating artery aneurysm rupture risk assessment. Neurosurgery 63( Suppl 1):163-164, 2016   20. Meng H, Tutino VM, Xiang J, Siddiqui A : High WSS or low WSS? Complex interactions of hemodynamics with intracranial aneurysm initiation, growth, and rupture: toward a unifying hypothesis. AJNR Am J Neuroradiol 35 : 1254-1262, 2014    21. Miura Y, Ishida F, Umeda Y, Tanemura H, Suzuki H, Matsushima S, et al : Low wall shear stress is independently associated with the rupture status of middle cerebral artery aneurysms. Stroke 44 : 519-521, 2013   22. Pereira VM, Brina O, Gonzalez AM, Narata AP, Ouared R, Karl-Olof L : Biology and hemodynamics of aneurismal vasculopathies. Eur J Radiol 82 : 1606-1617, 2013   23. Qian Y, Takao H, Umezu M, Murayama Y : Risk analysis of unruptured aneurysms using computational fluid dynamics technology: preliminary results. AJNR Am J Neuroradiol 32 : 1948-1955, 2011    24. Shojima M, Oshima M, Takagi K, Torii R, Hayakawa M, Katada K, et al : Magnitude and role of wall shear stress on cerebral aneurysm: computational fluid dynamic study of 20 middle cerebral artery aneurysms. Stroke 35 : 2500-2505, 2004   25. Sugiyama S, Meng H, Funamoto K, Inoue T, Fujimura M, Nakayama T, et al : Hemodynamic analysis of growing intracranial aneurysms arising from a posterior inferior cerebellar artery. World Neurosurg 78 : 462-468, 2012   26. Takao H, Murayama Y, Otsuka S, Qian Y, Mohamed A, Masuda S, et al : Hemodynamic differences between unruptured and ruptured intracranial aneurysms during observation. Stroke 43 : 1436-1439, 2012   27. Taylor CA, Hughes TJ, Zarins CK : Finite element modeling of three-dimensional pulsatile flow in the abdominal aorta: relevance to atherosclerosis. Ann Biomed Eng 26 : 975-987, 1998   28. Ujiie H, Tachibana H, Hiramatsu O, Hazel AL, Matsumoto T, Ogasawara Y, et al : Effects of size and shape (aspect ratio) on the hemodynamics of saccular aneurysms: a possible index for surgical treatment of intracranial aneurysms. Neurosurgery 45 : 119-129; discussion 129-130, 1999   29. Ujiie H, Tamano Y, Sasaki K, Hori T : Is the aspect ratio a reliable index for predicting the rupture of a saccular aneurysm? Neurosurgery 48 : 495-502; discussion 502-503, 2001   30. Xiang J, Natarajan SK, Tremmel M, Ma D, Mocco J, Hopkins LN, et al : Hemodynamic-morphologic discriminants for intracranial aneurysm rupture. Stroke 42 : 144-152, 2011   31. Xiang J, Yu J, Choi H, Dolan Fox JM, Snyder KV, Levy EI, et al : Rupture Resemblance Score (RRS): toward risk stratification of unruptured intracranial aneurysms using hemodynamic-morphological discriminants. J Neurointerv Surg 7 : 490-495, 2015   32. Xiang J, Yu J, Snyder KV, Levy EI, Siddiqui AH, Meng H : Hemodynamic-morphological discriminant models for intracranial aneurysm rupture remain stable with increasing sample size. J Neurointerv Surg 8 : 104-110, 2016   33. Zhang Y, Jing L, Liu J, Li C, Fan J, Wang S, et al : Clinical, morphological, and hemodynamic independent characteristic factors for rupture of posterior communicating artery aneurysms. J Neurointerv Surg 8 : 808-812, 2016   34. Zhang Y, Mu S, Chen J, Wang S, Li H, Yu H, et al : Hemodynamic analysis of intracranial aneurysms with daughter blebs. Eur Neurol 66 : 359-367, 2011  
|
|


















